숫자가 피보나치인지 테스트
피보나치 수 목록을 만드는 방법을 알고 있지만 주어진 숫자가 피보나치 목록에 속하는지 어떻게 테스트 할 수 있는지 모르겠습니다. 염두에 두는 한 가지 방법은 fib 목록을 생성하는 것입니다. 그 숫자까지 숫자를 입력하고 그것이 배열에 속하는지 확인하십시오. 그러나 더 간단하고 빠른 또 다른 방법이 있어야합니다.
어떤 아이디어?
아주 좋은 테스트는 N은 피보나치 수의 경우에만, 점이다 5 N^2 + 4또는 5N^2 – 4정사각형 숫자입니다. 숫자가 정사각형인지 효율적으로 테스트하는 방법에 대한 아이디어는 SO 토론을 참조하십시오 .
도움이 되었기를 바랍니다
그리고 경우에만 5ω 중 하나가 양의 정수 ω는 피보나치 수를 2 + 4 5ω 2 (4)는 완벽한 정사각형 -.
자세한 내용은 The Faboulous Fibonacci Numbers 를 참조하십시오.

여러 사람이 완전 제곱 해를 지적하지만 피보나치 수를 제곱하여 종종 거대한 제품을 생성합니다.
표준 64 비트 정수에 담을 수있는 피보나치 수는 80 개 미만입니다.
테스트 할 수보다 완전히 작게 작동하는 내 솔루션 이 있습니다.
( double및 같은 기본 유형을 사용하여 C #으로 작성되었습니다 long. 그러나 알고리즘은 더 큰 유형에 대해 잘 작동합니다.)
static bool IsFib(long T, out long idx)
{
double root5 = Math.Sqrt(5);
double phi = (1 + root5) / 2;
idx = (long)Math.Floor( Math.Log(T*root5) / Math.Log(phi) + 0.5 );
long u = (long)Math.Floor( Math.Pow(phi, idx)/root5 + 0.5);
return (u == T);
}
이 답변을 작성한 지 4 년이 지난 후 한 댓글 작성자가
out.
매개 변수 # 2는 피보나치 수열의 "색인"입니다.
테스트 할 값 T이 피보나치 수이면 idx피보나치 수열에서 해당 수의 1 기반 인덱스가됩니다. (한 가지 주목할만한 예외가 있음)
피보나치 수열은 1 1 2 3 5 8 13등입니다.
3은 수열에서 네 번째 숫자입니다 : IsFib(3, out idx);will return true및 value 4.
8은 시퀀스에서 6 번째 숫자입니다. IsFib(8, out idx);will return true및 value 6.
13은 7 번째 숫자입니다. IsFib(13, out idx);반환 true및 값 7.
한 가지 예외는이며 IsFib(1, out idx);, 2값 1이 인덱스 1과 2에 모두 표시 되더라도 반환 됩니다.
경우 IsFib비 피보나치 수를 전달, 그것은 반환 false, 그리고 값 idx보다 가장 큰 피보나치 수의 인덱스가됩니다 T.
16은 피보나치 값이 아닙니다. IsFib(16, out idx);반환 false및 값 7. Binet의 공식 을
사용 하여 인덱스 7을 16보다 작은 가장 큰 숫자 인 피보나치 값 13으로 변환 할 수 있습니다 .
#!/bin/bash
victim="144"
curl http://aux.planetmath.org/files/objects/7680/fib.txt | sed 's/^[0-9]*//;s/[ \t]//g' | grep "^$victim$" >/dev/null 2>/dev/null
if [[ $? -eq 0 ]] ; then
echo "$victim is a fibonacci number"
else
echo "$victim aint"
fi
숫자가 제한된 크기 인 경우 단순히 상한 아래의 모든 피보나치 숫자를 해시 테이블에 넣는 것보다 격리 테스트가 트릭을 수행합니다. 피보나치 수는 기하 급수적으로 증가하기 때문에 매우 적습니다 (예 : 5mln 미만 38 개).
숫자가 제한된 크기 가 아닌 경우 제곱 테스트를 사용하는 제안 된 트릭은 숫자를 찾거나 초과 할 때까지 피보나치 수열을 생성하는 것보다 거의 확실히 느립니다.
해결책을 위해 Binet의 Formula를 살펴보십시오.
( Wikipedia의 Fibonacci Number 에서 "Closed-Form Expression"을 찾으십시오. )
피보나치 수의 시퀀스는 간단한 닫힌 공식에 의해 생성됩니다.
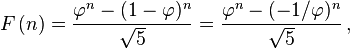
를 풀고 정수 n인지 테스트하면 n답을 얻을 수 있다고 믿습니다 .
편집 으로 같은 위키 백과 문서는 피보나치 수의 검출에 대한 섹션을 가지고 점을 @psmears. Wikipedia는 훌륭한 소스입니다.
양의 정수 ω는 피보나치 수입니다.
그리고 경우에만 경우 중 하나 5ω 2 + 4 5ω 2 - 4는 정사각형이다
에서 알프레드 Posamentier 및 잉마르 레만에 의해 (멋진) 피보나치 수
bool isFibonacci(int w)
{
double X1 = 5 * Math.Pow(w, 2) + 4;
double X2 = 5 * Math.Pow(w, 2) - 4;
long X1_sqrt = (long)Math.Sqrt(X1);
long X2_sqrt = (long)Math.Sqrt(X2);
return (X1_sqrt*X1_sqrt == X1) || (X2_sqrt*X2_sqrt == X2) ;
}
1k과 사이의 피보나치 수를 인쇄하는 스 니펫 10k.
for (int i = 1000; i < 10000; i++)
{
if (isFibonacci(i))
Console.Write(" "+i);
}
OMG 4 개 밖에 없어요 !!!
다른 방법으로
from math import *
phi = 1.61803399
sqrt5 = sqrt(5)
def F(n):
return int((phi**n - (1-phi)**n) /sqrt5)
def isFibonacci(z):
return F(int(floor(log(sqrt5*z,phi)+0.5))) == z
print [i for i in range(1000,10000) if isFibonacci(i)]
피보나치 수에 대한 위키피디아 문서의 "피보나치 수 인식"섹션을 참조하십시오 .
피보나치 수는 기하 급수적으로 증가하기 때문에 제안하는 방법은 매우 빠릅니다. 또 하나는 이것 입니다.
나와 psmears의 이전 답변을 기반 으로이 C # 코드를 작성했습니다.
단계를 천천히 거치며 명확하게 줄이고 최적화 할 수 있습니다.
// Input: T: number to test.
// Output: idx: index of the number in the Fibonacci sequence.
// eg: idx for 8 is 6. (0, 1, 1, 2, 3, 5, 8)
// Return value: True if Fibonacci, False otherwise.
static bool IsFib(long T, out int idx)
{
double root5 = Math.Sqrt(5);
double PSI = (1 + root5) / 2;
// For reference, IsFib(72723460248141) should show it is the 68th Fibonacci number
double a;
a = T*root5;
a = Math.Log(a) / Math.Log(PSI);
a += 0.5;
a = Math.Floor(a);
idx = (Int32)a;
long u = (long)Math.Floor(Math.Pow(PSI, a)/root5 + 0.5);
if (u == T)
{
return true;
}
else
{
idx = 0;
return false;
}
}
테스트 결과 처음 69 개의 피보나치 수에 대해 작동하지만 70 번째에 대해서는 분해됩니다.
F(69) = 117,669,030,460,994 - Works
F(70) = 190,392,490,709,135 - Fails
대체로 어떤 종류의 BigInt 라이브러리를 사용하지 않는 한, 알고리즘을 실행하는 것보다 피보나치 숫자의 간단한 조회 테이블을 가지고 확인하는 것이 좋습니다.
처음 300 개의 번호 목록은 온라인에서 쉽게 확인할 수 있습니다.
그러나이 코드는 충분한 정밀도가 있고 숫자 표현 시스템을 오버플로하지 않는 경우 실행 가능한 알고리즘을 설명합니다.
Wikipedia에서 : http://en.wikipedia.org/wiki/Fibonacci_number
양의 정수 z는 5z ^ 2 + 4 또는 5z ^ 2 − 4 중 하나가 완전 제곱 인 경우에만 피보나치 수입니다.
Re : Ahmad의 코드-재귀 나 포인터가없는 더 간단한 접근 방식, 상당히 순진하지만 정말 거대한 숫자 (최신 기계에서는 밀리 초가 걸리는 N 번째 fib 번호를 확인하기 위해 대략 2N 추가)가 필요하지 않습니다. 아무리 나빠도)
// 무언가를 찾으면 pos를 반환하고, 찾지 못하면 0을 반환합니다 (C / C ++는 모든 값을! = 0으로 처리하므로 동일한 최종 결과).
int isFib (long n)
{
int pos = 2;
long last = 1;
long current = 1;
long temp;
while (current < n)
{
temp = last;
last = current;
current = current + temp;
pos++;
}
if (current == n)
return pos;
else
return 0;
}
피보나치 수에 대한 일반적인 표현은 F (n) = [[(1 + sqrt (5)) / 2] sup n + 1-[(1-sqrt (5)) / 2] sup n + 1] / sqrt입니다. (5) ..... (*) 두 번째 지수는 큰 n에 대해 0이되고 수치 연산을 수행하면 F (n) = [(1.618) sup n + 1] / 2.236
K가 테스트 할 숫자이면 log (k * 2.2336) / log (1.618)는 정수 여야합니다!
K가 13 인 경우 내 계산기는 7.00246 답을 제공합니다. K가 14 인 경우 답은 7.1564입니다.
답에 가장 가까운 정수를 취하고 (*)로 대체하여 결과가 K인지 확인하여 결과의 신뢰도를 높일 수 있습니다.
당신이 다루는 숫자는 얼마나 큽니까?
조회 테이블이 도움이 될 수 있습니까? (검색 할 수있는 미리 계산 된 숫자 목록)
분석적으로 답을 얻기 위해 뒤집을 수 있는 폐쇄 형 표현 도 있습니다 (나는 수학자는 아니지만이 제안이 의미가 있다고 약속 할 수는 없습니다)
간단한 추가, 배열 사전 계산, 결과를 해시로 메모하는 것과 함께 여기에 제시된 방법에 대한 몇 가지 벤치 마크를 실행했습니다. Perl의 경우 적어도 제곱 방법은 로그 방법보다 약간 빠르며 아마도 20 % 더 빠릅니다. abelenky가 지적했듯이, 비트 수를 제곱 할 여지가 있는지 여부 사이의 상충 관계입니다.
확실히 가장 빠른 방법은 도메인 공간의 모든 피보나치 수를 해시하는 것입니다. abelenky가 만드는 또 다른 점의 선을 따라 2 ^ 64보다 작은이 빨판은 94 개뿐입니다.
미리 계산하고 Perl 해시, Python 사전 등에 넣어야합니다.
피보나치 수의 속성은 매우 흥미롭지 만 컴퓨터 프로그램의 정수가 하나인지 여부를 결정하는 데 사용하는 것은 프로그램이 시작될 때마다 pi를 계산하는 서브 루틴을 작성하는 것과 같습니다.
이것이 벤치 마크인지 확실하지 않은 내 솔루션입니다. 이게 도움이 되길 바란다!
def is_fibonacci?(i)
a,b=0,1
until b >= i
a,b=b,a+b
return true if b == i
end
end
무엇을 A, B는 = B는 + b를 하고있다
0, 1 = 1, 0 +1
1, 1 = 1, 1 + 1
1, 2 = 2, 1 + 2
2, 3 = 3, 2 + 3
fib1 = fib2
fib2 = fib1 + fib2
스칼라 버전
def isFib(n: Int): Boolean = {
def checkFib(f1: Int = 1, f2: Int = 1): Boolean = {
if(n == f1 || n == f2) true
else if(n < f2) false
else checkFib(f2, f1+f2)
}
checkFib()
}
Java 솔루션은 다음과 같이 수행 할 수 있습니다. 하지만 여전히 최적화 할 수 있습니다.
다음 솔루션은
- 1≤T≤10 ^ 5
- 1≤N≤10 ^ 10
T는 테스트 케이스의 수, N은 수의 범위입니다.
import java.util.Scanner;
import java.math.BigDecimal;
import java.math.RoundingMode;
public class FibonacciTester {
private static BigDecimal zero = BigDecimal.valueOf(0);
private static BigDecimal one = BigDecimal.valueOf(1);
private static BigDecimal two = BigDecimal.valueOf(2);
private static BigDecimal four = BigDecimal.valueOf(4);
private static BigDecimal five = BigDecimal.valueOf(5);
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
BigDecimal[] inputs = new BigDecimal[n];
for (int i = 0; i < n; i++) {
inputs[i] = sc.nextBigDecimal();
}
for (int i = 0; i < inputs.length; i++) {
if (isFibonacci(inputs[i]))
System.out.println("IsFibo");
else
System.out.println("IsNotFibo");
}
}
public static boolean isFibonacci(BigDecimal num) {
if (num.compareTo(zero) <= 0) {
return false;
}
BigDecimal base = num.multiply(num).multiply(five);
BigDecimal possibility1 = base.add(four);
BigDecimal possibility2 = base.subtract(four);
return (isPerfectSquare(possibility1) || isPerfectSquare(possibility2));
}
public static boolean isPerfectSquare(BigDecimal num) {
BigDecimal squareRoot = one;
BigDecimal square = one;
BigDecimal i = one;
BigDecimal newSquareRoot;
int comparison = -1;
while (comparison != 0) {
if (comparison < 0) {
i = i.multiply(two);
newSquareRoot = squareRoot.add(i).setScale(0, RoundingMode.HALF_UP);
} else {
i = i.divide(two);
newSquareRoot = squareRoot.subtract(i).setScale(0, RoundingMode.HALF_UP);
}
if (newSquareRoot.compareTo(squareRoot) == 0) {
return false;
}
squareRoot = newSquareRoot;
square = squareRoot.multiply(squareRoot);
comparison = square.compareTo(num);
}
return true;
}
}
int isfib(int n /* number */, int &pos /* position */)
{
if (n == 1)
{
pos=2; // 1 1
return 1;
}
else if (n == 2)
{
pos=3; // 1 1 2
return 1;
}
else
{
int m = n /2;
int p, q, x, y;
int t1=0, t2 =0;
for (int i = m; i < n; i++)
{
p = i;
q = n -p; // p + q = n
t1 = isfib(p, x);
if (t1) t2 = isfib(q, y);
if (t1 && t2 && x == y +1)
{
pos = x+1;
return 1; //true
}
}
pos = -1;
return 0; //false
}
}
이것은 어떤가요?
#include <stdio.h>
#include <math.h>
int main()
{
int number_entered, x, y;
printf("Please enter a number.\n");
scanf("%d", &number_entered);
x = y = 5 * number_entered^2 + 4; /*Test if 5N^2 + 4 is a square number.*/
x = sqrt(x);
x = x^2;
if (x == y)
{
printf("That number is in the Fibonacci sequence.\n");
}
x = y = 5 * number_entered^2 - 4; /*Test if 5N^2 - 4 is a square number.*/
x = sqrt(x);
x = x^2;
if (x == y)
{
printf("That number is in the Fibonacci sequence.\n");
}
else
{
printf("That number isn't in the Fibonacci sequence.\n");
}
return 0;
}
작동할까요?
참고 URL : https://stackoverflow.com/questions/2432669/test-if-a-number-is-fibonacci
'Programing' 카테고리의 다른 글
| Ruby로 XLS 및 XLSX (MS Excel) 파일 구문 분석? (0) | 2020.10.28 |
|---|---|
| PHP에서 에코 내에 줄 바꿈을 추가하는 방법은 무엇입니까? (0) | 2020.10.28 |
| Mac OS X Lion에서`gem install therubyracer` 실패 (0) | 2020.10.28 |
| Qt에서 경과 시간 가져 오기 (0) | 2020.10.28 |
| java.lang.IllegalArgumentException : 유형의 반환 값에 대한 변환기가 없습니다. (0) | 2020.10.28 |